最新平面向量的数量积及运算率课件PPT课件 26页

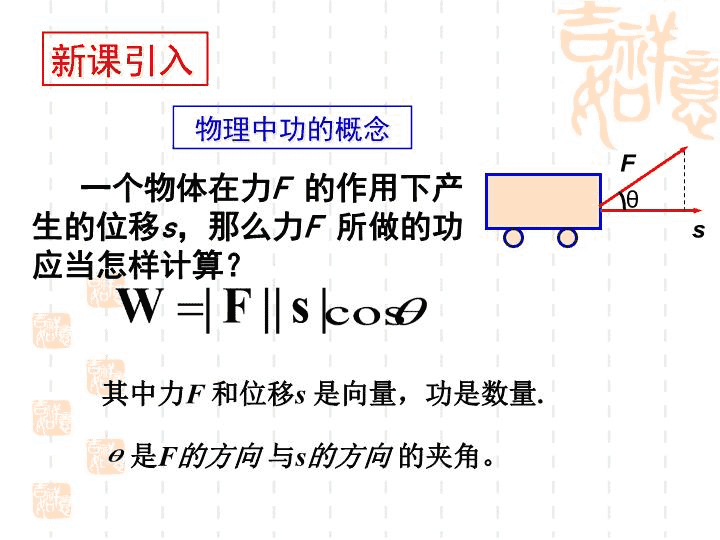
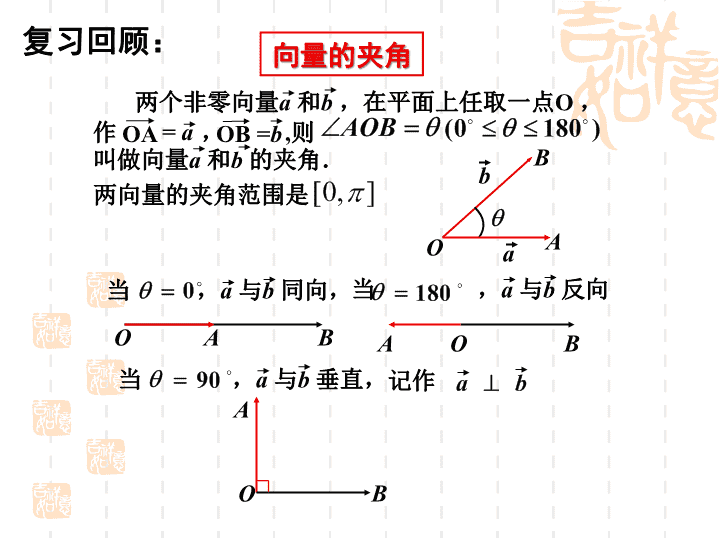
'平面向量的数量积及运算率课件 向量的夹角两向量的夹角范围是两个非零向量a和b，在平面上任取一点O，作，,则叫做向量a和b的夹角．OB=bOA=a记作当，a与b垂直，当，a与b同向，当，a与b反向AOBOABBabAOOAB复习回顾： 两个向量的数量积的性质（判断向量垂直） 解：a·b=|a||b|cosθ=5×4×cos120°=5×4×（-1/2）=－10例1已知|a|=5，|b|=4，a与b的夹角θ=120°，求a·b。 二、平面向量的数量积的运算律：数量积的运算律：其中，是任意三个向量，注： 则(a+b)·c=ON|c|=(OM+MN)|c|=OM|c|+MN|c|=a·c+b·c.ONMa+bbac向量a、b、a+b在c上的射影的数量分别是OM、MN、ON,证明运算律(3) 例2：求证：（1）(a＋b)2＝a2＋2a·b＋b2；（2）(a＋b)·(a－b)＝a2－b2.证明：（1）(a＋b)2＝(a＋b)·(a＋b)＝(a＋b)·a＋(a＋b)·b＝a·a＋b·a＋a·b＋b·b＝a2＋2a·b＋b2. 例2：求证：（2）(a＋b)·(a－b)＝a2－b2.证明：（2）(a＋b)·(a－b)＝(a＋b)·a－(a＋b)·b＝a·a＋b·a－a·b－b·b＝a2－b2. 例3已知a=(1,1),b=(2,0),求a·b。解：|a|=|b|=2,θ=45°∴a·b=|a||b|cosθ=×2×cos45°=2 例4 例5 总结提炼1、向量的数量积的物理模型是力的做功；4、两向量的夹角范围是5、掌握五条重要性质：平面向量的数量积的几何意义是:a的长度|a|与b在a的方向上的投影|b|cos的乘积2、a·b的结果是一个实数，它是标量不是向量。3、利用a·b=|a|·|b|cos可求两向量的夹角，尤其是判定垂直。 当堂练习：1．若a=0，则对任一向量b，有a·b=0．2．若a≠0，则对任一非零向量b,有a·b≠0．3．若a≠0，a·b=0，则b=04．若a·b=0，则a·b中至少有一个为0．5．若a≠0，a·b=b·c，则a=c6．若a·b=a·c,则b≠c,当且仅当a=0时成立．7．对任意向量a有√×××××√ CAB60。5824-20D 3或－3 已知与的夹角为60°，求：（1）在方向上的投影；（2）在方向上的投影；（3）（4）（5） 小结：1.2.可用来求向量的模3.投影 布置作业《成才之路》谢谢再见 结束语谢谢大家聆听！！！26'