最新偏置、摆动、平底从动件盘形凸轮轮廓设计课件PPT.ppt 78页

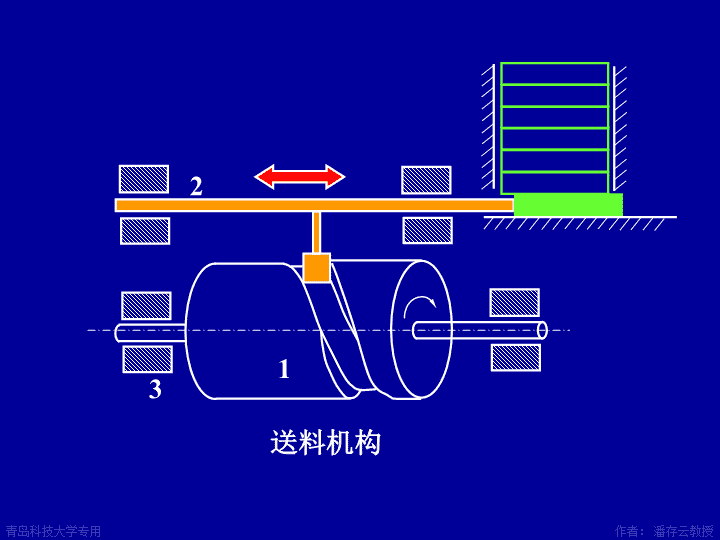
'偏置、摆动、平底从动件盘形凸轮轮廓设计 作者：潘存云教授作者：潘存云教授132送料机构青岛科技大学专用作者：潘存云教授 作者：潘存云教授δ’0δ’0otδs§9－2推杆的运动规律凸轮机构设计的基本任务:1)根据工作要求选定凸轮机构的形式;名词术语：一、推杆的常用运动规律基圆、推程运动角、基圆半径、推程、远休止角、回程运动角、回程、近休止角、行程。一个循环r0hωA而根据工作要求选定推杆运动规律，是设计凸轮轮廓曲线的前提。2)推杆运动规律;3)合理确定结构尺寸;4)设计轮廓曲线。δ01δ01δ02δ02DBCB’δ0δ0青岛科技大学专用作者：潘存云教授 2.二次多项式（等加等减速）运动规律位移曲线为一抛物线。加、减速各占一半。推程加速上升段边界条件：起始点：δ=0，s=0，v＝0中间点：δ=δ0/2，s=h/2求得：C0＝0，C1＝0，C2＝2h/δ20加速段推程运动方程为：s＝2hδ2/δ20v＝4hωδ/δ20a＝4hω2/δ20青岛科技大学专用作者：潘存云教授 作者：潘存云教授δah/2δ0h/2推程减速上升段边界条件：终止点：δ=δ0，s=h，v＝0中间点：δ=δ0/2，s=h/2求得：C0＝－h，C1＝4h/δ0C2＝-2h/δ20减速段推程运动方程为：s＝h-2h(δ0–δ)2/δ201δsv＝-4hω(δ0-δ)/δ20a＝-4hω2/δ20235462hω/δ0柔性冲击4hω2/δ203重写加速段推程运动方程为：s＝2hδ2/δ20v＝4hωδ/δ20a＝4hω2/δ20δv青岛科技大学专用作者：潘存云教授 同理可得回程等加速段的运动方程为：s＝h-2hδ2/δ’20v＝-4hωδ/δ’20a＝-4hω2/δ’20回程等减速段运动方程为：s＝2h(δ’0-δ)2/δ’20v＝-4hω(δ’0-δ)/δ’20a＝4hω2/δ’20青岛科技大学专用作者：潘存云教授 3.五次多项式运动规律s=10h(δ/δ0)3－15h(δ/δ0)4+6h(δ/δ0)5δsvahδ0无冲击，适用于高速凸轮。v=ds/dt=C1ω+2C2ωδ+3C3ωδ2+4C4ωδ3+5C5ωδ4a=dv/dt=2C2ω2+6C3ω2δ+12C4ω2δ2+20C5ω2δ3一般表达式：边界条件：起始点：δ=0，s=0，v＝0，a＝0终止点：δ=δ0，s=h,v＝0，a＝0求得：C0＝C1＝C2＝0,C3＝10h/δ03,C4＝15h/δ04,C5＝6h/δ05s=C0+C1δ+C2δ2+C3δ3+C4δ4+C5δ5位移方程：青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云hδ0δsδa二、三角函数运动规律1.余弦加速度(简谐)运动规律推程：s＝h[1-cos(πδ/δ0)]/2v＝πhωsin(πδ/δ0)δ/2δ0a＝π2hω2cos(πδ/δ0)/2δ20回程：s＝h[1＋cos(πδ/δ’0)]/2v＝-πhωsin(πδ/δ’0)δ/2δ’0a＝-π2hω2cos(πδ/δ’0)/2δ’20123456δvVmax=1.57hω/2δ0在起始和终止处理论上a为有限值，产生柔性冲击。123456青岛科技大学专用作者：潘存云教授 作者：潘存云教授sδδaδvhδ02.正弦加速度（摆线）运动规律推程：s＝h[δ/δ0-sin(2πδ/δ0)/2π]v＝hω[1-cos(2πδ/δ0)]/δ0a＝2πhω2sin(2πδ/δ0)/δ20回程：s＝h[1-δ/δ’0+sin(2πδ/δ’0)/2π]v＝hω[cos(2πδ/δ’0)-1]/δ’0a＝-2πhω2sin(2πδ/δ’0)/δ’20无冲击vmax=2hω/δ0amax=6.28hω2/δ02123456r=h/2πθ=2πδ/δ0青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云vsaδδδhoooδ0三、改进型运动规律将几种运动规律组合，以改善运动特性。+∞-∞正弦改进等速vsaδδδhoooδ0青岛科技大学专用作者：潘存云教授 作者：潘存云教授四、选择运动规律选择原则：1.机器的工作过程只要求凸轮转过一角度δ0时，推杆完成一行程h（直动推杆）或φ（摆动推杆），对运动规律并无严格要求。则应选择直线或圆弧等易加工曲线作为凸轮的轮廓曲线。如夹紧凸轮。ω工件工件ωφδ0青岛科技大学专用作者：潘存云教授 作者：潘存云教授四、选择运动规律选择原则：2.机器的工作过程对推杆运动有要求，则应严格按工作要求的运动规律来设计凸轮廓线。如刀架进给凸轮。3.对高速凸轮，要求有较好的动力特性，除了避免出现刚性或柔性冲击外，还应当考虑Vmax和amax。ωωhδ0青岛科技大学专用作者：潘存云教授 作者：潘存云教授高速重载凸轮要选Vmax和amax比较小的理由：②amax↑等加等减速2.04.0柔性中速轻载五次多项式1.885.77无高速中载余弦加速度1.574.93柔性中速中载正弦加速度2.06.28无高速轻载改进正弦加速度1.765.53无高速重载100分钟从动件常用运动规律特性比较运动规律Vmaxamax冲击推荐应用范围(hω/δ0)×(hω/δ20)×等速1.0∞刚性低速轻载→动量mv↑,若机构突然被卡住，则冲击力将很大（F=mv/t）。对重载凸轮，则适合选用Vmax较小的运动规律。→惯性力F=-ma↑对强度和耐磨性要求↑。对高速凸轮，希望amax愈小愈好。①Vmax↑,Pn↑青岛科技大学专用作者：潘存云教授 1.凸轮廓线设计方法的基本原理§9－3凸轮轮廓曲线的设计2.用作图法设计凸轮廓线1)对心直动尖顶推杆盘形凸轮2)对心直动滚子推杆盘形凸轮3)对心直动平底推杆盘形凸轮4)偏置直动尖顶推杆盘形凸轮5)摆动尖顶推杆盘形凸轮机构6)直动推杆圆柱凸轮机构7)摆动推杆圆柱凸轮机构3.用解析法设计凸轮的轮廓曲线青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云一、凸轮廓线设计方法的基本原理反转原理：依据此原理可以用几何作图的方法设计凸轮的轮廓曲线，例如：给整个凸轮机构施以-ω时，不影响各构件之间的相对运动，此时，凸轮将静止，而从动件尖顶复合运动的轨迹即凸轮的轮廓曲线。尖顶凸轮绘制动画滚子凸轮绘制动画O-ω3’1’2’331122ω青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云60°r0120°-ωω1’已知凸轮的基圆半径r0，角速度ω和从动件的运动规律，设计该凸轮轮廓曲线。设计步骤小结：①选比例尺μl作基圆r0。②反向等分各运动角。原则是：陡密缓疏。③确定反转后，从动件尖顶在各等份点的位置。④将各尖顶点连接成一条光滑曲线。1.对心直动尖顶从动件盘形凸轮1’3’5’7’8’2’3’4’5’6’7’8’9’10’11’12’13’14’90°90°A1876543214131211109二、直动从动件盘形凸轮轮廓的绘制60°120°90°90°135789111315sδ9’11’13’12’14’10’青岛科技大学专用作者：潘存云教授 作者：潘存云教授2)对心直动滚子推杆盘形凸轮设计：潘存云sδ911131513578r0A120°-ω1’设计步骤小结：①选比例尺μl作基圆r0。②反向等分各运动角。原则是：陡密缓疏。③确定反转后，从动件尖顶在各等份点的位置。④将各尖顶点连接成一条光滑曲线。1’3’5’7’8’9’11’13’12’14’2’3’4’5’6’7’8’9’10’11’12’13’14’60°90°90°1876543214131211109理论轮廓实际轮廓⑤作各位置滚子圆的内(外)包络线。已知凸轮的基圆半径r0，角速度ω和从动件的运动规律，设计该凸轮轮廓曲线。60°120°90°90°ω青岛科技大学专用作者：潘存云教授 作者：潘存云教授3)对心直动平底推杆盘形凸轮设计：潘存云sδ911131513578r08’7’6’5’4’3’2’1’9’10’11’12’13’14’-ωωA1’3’5’7’8’9’11’13’12’14’12345678151413121110960°120°90°90°平底从动件盘形凸轮轮廓的设计思路与滚子直动从动件盘形凸轮轮廓相似，取从动件导路与平底的交点A作为参考点。按照尖顶从动件盘形凸轮轮廓的设计方法，求出反转后参考点所占据的一系列位置。青岛科技大学专用作者：潘存云教授 作者：潘存云教授3)对心直动平底推杆盘形凸轮设计：潘存云sδ911131513578r08’7’6’5’4’3’2’1’9’10’11’12’13’14’-ωωA1’3’5’7’8’9’11’13’12’14’12345678151413121110960°120°90°90°再过这一系列点画出一系列代表平底在反转后各个位置的直线族，最后作直线族的包络线，就是凸轮的实际轮廓。青岛科技大学专用作者：潘存云教授 作者：潘存云教授3)对心直动平底推杆盘形凸轮设计：潘存云r0应当指出，如果凸轮的实际轮廓不能与每个平底相切，会导致从动件不能实现预定的运动规律，产生运动失真。此时可增大凸轮的基圆半径，重新绘制凸轮轮廓。8’7’6’5’4’3’2’1’9’10’11’12’13’14’-ωωA123456781514131211109青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云911131513578OeA已知凸轮的基圆半径r0，角速度ω和从动件的运动规律和从动件导路偏置于凸轮轴心的右侧，偏心距e，设计该凸轮轮廓曲线。4)偏置直动尖顶从动件盘形凸轮1’3’5’7’8’9’11’13’12’14’-ωω6’1’2’3’4’5’7’8’15’14’13’12’11’10’9’1514131211109k9k10k11k12k13k14k1512345678k1k2k3k5k4k6k7k860°120°90°90°s2δ青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云911131513578OeA首先，根据给定的从动件运动规律，绘制出从动件位移线图，并且对位移线图的横坐标的推程和回程分成若干等份，得到等分点1，2，、、、15，如图所示。4)偏置直动尖顶从动件盘形凸轮1’3’5’7’8’9’11’13’12’14’-ωω6’1’2’3’4’5’7’8’15’14’13’12’11’10’9’1514131211109k9k10k11k12k13k14k1512345678k1k2k3k5k4k6k7k860°120°90°90°s2δ青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云911131513578OeA其次，以给定的基圆半径和偏距为半径，绘制出以凸轮轴心O为圆心的基圆和偏距圆，找到从动件导路在起始位置时与偏距圆的切点。4)偏置直动尖顶从动件盘形凸轮1’3’5’7’8’9’11’13’12’14’-ωω6’1’2’3’4’5’7’8’15’14’13’12’11’10’9’1514131211109k9k10k11k12k13k14k1512345678k1k2k3k5k4k6k7k860°120°90°90°s2δ青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云911131513578OeA从起始切点开始，按照顺时针的方向将偏距圆的运动行程部分作与位移线图横坐标对应的等份，并且过这些等分点作偏距圆的切线，依次交基圆与1，2，、、、15各点。4)偏置直动尖顶从动件盘形凸轮1’3’5’7’8’9’11’13’12’14’-ωω6’1’2’3’4’5’7’8’15’14’13’12’11’10’9’1514131211109k9k10k11k12k13k14k1512345678k1k2k3k5k4k6k7k860°120°90°90°s2δ青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云911131513578OeA最后，在上述切线上从基圆起向外截取线段，使它们依次等于位移线图运动行程部分对应的各纵坐标，得到的点即代表在反转运动中从动件尖顶的一系列位置。将这些点连成光滑曲线，即得所求的凸轮轮廓。4)偏置直动尖顶从动件盘形凸轮1’3’5’7’8’9’11’13’12’14’-ωω6’1’2’3’4’5’7’8’15’14’13’12’11’10’9’1514131211109k9k10k11k12k13k14k1512345678k1k2k3k5k4k6k7k860°120°90°90°s2δ青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云120°B’1φ1r060°120°90°90°yδ已知凸轮的基圆半径r0，角速度ω，摆杆长度l以及摆杆回转中心与凸轮回转中心的距离d，摆动从动件盘形凸轮机构运动规律，凸轮以等角速度逆时针方向转动，摆杆在推程作顺时针方向摆动，设计该凸轮轮廓曲线。1’2’3’4’56785’6’7’8’B1B2B3B4B5B6B7B860°90°ω-ωdABl1234B’2φ2B’3φ3B’4φ4B’5φ5B’6φ6B’7φ7A1A2A3A4A5A6A7A85)摆动尖顶推杆盘形凸轮机构青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云120°B’1φ1r060°120°90°90°yδ首先，根据给定的从动件运动规律，绘制出从动件角位移线图，并且对位移线图横坐标的推程和回程分成若干等份，得到等分点1，2，、、、8，这时各等分点的纵坐标代表摆杆对应于凸轮各运动角的角位移。1’2’3’4’56785’6’7’8’B1B2B3B4B5B6B7B860°90°ω-ωdABl1234B’2φ2B’3φ3B’4φ4B’5φ5B’6φ6B’7φ7A1A2A3A4A5A6A7A8青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云120°B’1φ1r060°120°90°90°yδ其次，以给定的基圆半径和中心距为半径，绘制出以凸轮轴心O为圆心的基圆和摆轴圆。以摆轴的起始位置A为圆心，摆杆长度为半径，作圆弧交基圆于B点，AB即是摆杆的起始位置。从A点开始，按照顺时针方向将摆轴圆的运动行程部分作与角位移线图横坐标对应的等分，得到A1，A2，、、、A8各点。1’2’3’4’56785’6’7’8’B1B2B3B4B5B6B7B860°90°ω-ωdABl1234B’2φ2B’3φ3B’4φ4B’5φ5B’6φ6B’7φ7A1A2A3A4A5A6A7A8青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云120°B’1φ1r060°120°90°90°yδ再分别以A1，A2，、、、A8各点为圆心，摆杆长度为半径，作圆弧分别交基圆于B1，B2，、、、B8各点，得到线段A1B1，A2B2，、、、A8B8。1’2’3’4’56785’6’7’8’B1B2B3B4B5B6B7B860°90°ω-ωdABl1234B’2φ2B’3φ3B’4φ4B’5φ5B’6φ6B’7φ7A1A2A3A4A5A6A7A8青岛科技大学专用作者：潘存云教授 作者：潘存云教授设计：潘存云120°B’1φ1r060°120°90°90°yδ1’2’3’4’56785’6’7’8’B1B2B3B4B5B6B7B860°90°ω-ωdABl1234B’2φ2B’3φ3B’4φ4B’5φ5B’6φ6B’7φ7A1A2A3A4A5A6A7A8最后，依次以线段A1B1，A2B2，、、、为一边，作角f1，f2，、、、f7分别等于角位移线图的纵坐标，得到一系列点，它们即代表在反转运动中摆杆尖顶的一系列位置。将这些点连成光滑曲线，即得所求的凸轮轮廓。青岛科技大学专用作者：潘存云教授 作者：潘存云教授作者：潘存云教授2πRV=ωRωvR－V6)直动推杆圆柱凸轮机构思路：将圆柱外表面展开，得一长度为2πR的平面移动凸轮机构，其移动速度为V=ωR，以－V反向移动平面凸轮，相对运动不变，滚子反向移动后其中心点的轨迹即为理论轮廓，其内外包络线为实际轮廓。Bv青岛科技大学专用作者：潘存云教授 作者：潘存云教授δs123456787’6’5’4’3’2’1’ββ"β"6)直动推杆圆柱凸轮机构已知：圆柱凸轮的半径R，从动件的运动规律，设计该圆柱凸轮机构。6’5’4’3’2’1’7’ωvR12345678V=ωR－Vs2πR青岛科技大学专用作者：潘存云教授 作者：潘存云教授作者：潘存云教授7)摆动推杆圆柱凸轮机构已知：圆柱凸轮的半径R，滚子半径rr从动件的运动规律，设计该凸轮机构。2”3”4”5”6”7”8”9”0”0”φ1”ω2rrAφ中线8’7’9’RδφV=ωR－V2πRA2A3A4A1A0A7A8A9A5A6A0A4’,5’,6’3’2’1’0’012345678902πR青岛科技大学专用作者：潘存云教授 作者：潘存云教授δyxB03.用解析法设计凸轮的轮廓曲线1)偏置直动滚子推杆盘形凸轮机构θ由图可知：s0＝(r02-e2)1/2实际轮廓线－为理论轮廓的等距线。曲线任意点切线与法线斜率互为负倒数：原理：反转法设计结果：轮廓的参数方程:x=x(δ)y=y(δ)x=(s0+s)sinδ+ecosδy=(s0+s)cosδ-esinδetgθ=-dx/dy=(dx/dδ)/(-dy/dδ)=sinθ/cosθ(1)er0-ωωrrr0s0snns0yxδδ已知：r0、rT、e、ω、S=S(δ)青岛科技大学专用作者：潘存云教授 作者：潘存云教授(x,y)rrnn对(1)式求导，得：dx/dδ＝(ds/dδ-e)sinδ+(s0+s)cosδ式中:“－”对应于内等距线，“＋”对应于外等距线。实际轮廓为B’点的坐标：x’=y’=x-rrcosθy-rrsinθδyxB0θeer0-ωωrrr0s0snns0yxδδ(dx/dδ)(dx/dδ)2+(dy/dδ)2得：sinθ=(dy/dδ)(dx/dδ)2+(dy/dδ)2cosθ=(x’,y’)θ(x’,y’)θdy/dδ＝(ds/dδ-e)cosδ-(s0+s)sinδ青岛科技大学专用作者：潘存云教授 作者：潘存云教授s0r0B0Oxyω(x,y)2)对心直动平底推杆盘形凸轮OP=v/ωy=x=建立坐标系如图：P点为相对瞬心，(r0+s)sinδ+(ds/dδ)cosδ(r0+s)cosδ－(ds/dδ)sinδv推杆移动速度为：=(ds/dt)/(dδ/dt)=ds/dδv=vp=OPω-ωδds/dδs0sPB反转δ后，推杆移动距离为S，δδ青岛科技大学专用作者：潘存云教授 作者：潘存云教授φ0xr0OyωlA0B03)摆动滚子推杆盘形凸轮机构已知：中心距a，摆杆长度l，φ0、ω、S=S(δ)理论廓线方程：x=y=实际轮廓方程的求法同前。asinδ－lsin(δ+φ+φ0)acosδ－lcos(δ+φ+φ0)lsin(δ+φ+φ0)asinδyxaδa对应点B’的坐标为：x’=xrrcosθy’=yrrsinθAδ-ωBφ0φacosδ青岛科技大学专用作者：潘存云教授 §9－4凸轮机构基本尺寸的确定上述设计廓线时的凸轮结构参数r0、e、rr等，是预先给定的。实际上，这些参数也是根据机构的受力情况是否良好、动作是否灵活、尺寸是否紧凑等因素由设计者确定的。1.凸轮机构的压力角2.凸轮基圆半径的确定3.滚子半径的确定4.平底尺寸l的确定青岛科技大学专用作者：潘存云教授 作者：潘存云教授lbBωd1.凸轮机构的压力角受力图中，由∑Fx=0，∑Fy=0，∑MB=0得：FR2FR1ttnnφ1φ2φ2α-Fsin(α+φ1)+(FR1－FR2)cosφ2=0－G+Fcos(α+φ1)－(FR1+FR2)sinφ2=0FR2cosφ2(l+b)－FR1cosφ2b=0由以上三式消去R1、R2得：vGF=cos(α+φ1)－(1+2b/l)sin(α+φ1)tgφ2G压力角----正压力与推杆上B点速度方向之间的夹角αα↑→分母↓→F↑若α大到使分母趋于0，则F→∞→机构发生自锁F青岛科技大学专用作者：潘存云教授 作者：潘存云教授称αc=arctg[1/(1+2b/l)tgφ2]-φ1为临界压力角。增大导轨长度l或减小悬臂尺寸b可提高αc工程上要求：αmax≤[α]直动推杆：[α]＝30°摆动推杆：[α]＝35°～45°回程：[α]’＝70°～80°提问：平底推杆α＝？nn0vOωr0青岛科技大学专用作者：潘存云教授 作者：潘存云教授BOωs0sDP点为相对瞬心：由△BCP得:2.凸轮基圆半径的确定ds/dδOP=v/ω=[ds/dt]/[dδ/dt]=[ds/dδ]运动规律确定之后，凸轮机构的压力角α与基圆半径r0直接相关。=(ds/dδ-e)/(s0+s)tgα=(OP-e)/BCnnPvvr0αe∴tgα=s+r20-e2ds/dδ-e其中：s0=r20-e2r0↑→α↓图示凸轮机构中，导路位于右侧。e↑→α↓青岛科技大学专用作者：潘存云教授 作者：潘存云教授OBω设计：潘存云αds/dδ∴tgα=s+r20-e2ds/dδ+enn同理，当导路位于中心左侧时，有：∴CP=ds/dδ+eePCr0s0sD=(ds/dδ+e)/(s0+s)tgα=(OP+e)/BC其中：s0=r20-e2e↑→α↑OP=v/ω=[ds/dt]/[dδ/dt]=[ds/dδ]此时，当偏距e增大时，压力角反而增大。对于直动推杆凸轮机构存在一个正确偏置的问题！青岛科技大学专用作者：潘存云教授 作者：潘存云教授作者：潘存云教授综合考虑两种情况有：tgα=s+r20-e2ds/dδ±e“+”用于导路和瞬心位于凸轮回转中心的两侧；显然，导路和瞬心位于中心同侧时，压力角将减小。注意：用偏置法可减小推程压力角，但同时增大了回程压力角，故偏距e不能太大。正确偏置：导路位于与凸轮旋转方向ω相反的位置。αoBω设计：潘存云nnPeB0ωnnPe正确偏置错误偏置α“-”用于导路和瞬心位于凸轮回转中心的同侧；青岛科技大学专用作者：潘存云教授 设计时要求：α≤[α]于是有：对心布置有：tgα=ds/dδ/(r0+s）提问：在设计一对心凸轮机构设计时，当出现α≥[α]的情况，在不改变运动规律的前提下，可采取哪些措施来进行改进？确定上述极值r0min不方便，工程上常根据诺模图来确定r0。见下页1)加大基圆半径r0，2)将对心改为偏置，3)采用平底从动件,tgα=(ds/dδ-e)/[(r02-e2)1/2+s]α=0r0↑→α↓e↑→α↓青岛科技大学专用作者：潘存云教授 作者：潘存云教授诺模图:应用实例：一对心直动滚子推杆盘形凸轮机构，δ0＝45º，h=13mm,推杆以正弦加速度运动，要求:αmax≦30º，试确定凸轮的基圆半径r0。作图得：h/r0＝0.26r0≧50mmh/r0等速运动0.010.10.20.30.40.50.60.81.02.03.05.0作者：潘存云教授h/r0等加等减速运动0.010.10.20.30.40.61.02.05.0凸轮转角δ05101525303540205060708090100100200300360最大压力角αmax510152520354555657585403050607080h/r0正弦加速度运动0.010.10.20.40.61.02.05.0作者：潘存云教授h/r0余弦加速度运动0.010.10.20.40.61.02.05.0510152520354555657585403050607080最大压力角αmax5101525303540205060708090100100200300360凸轮转角δ0h/r0正弦加速度运动0.010.10.20.40.61.02.05.0青岛科技大学专用作者：潘存云教授 作者：潘存云教授作者：潘存云教授设计：潘存云ρa－工作轮廓的曲率半径，ρ－理论轮廓的曲率半径，rT－滚子半径ρrT轮廓失真3.滚子半径的确定ρa＝ρ＋rTρ＝rTρa＝ρ－rT＝0轮廓正常轮廓变尖ρ内凹ρarTrTρrTρρ>rTρa＝ρ－rT轮廓正常外凸rTρaρ青岛科技大学专用作者：潘存云教授 可用求极值的方法求得ρmin,常采用上机编程求得ρmin工程上要求ρa≥1～5曲线之曲率半径：ρ＝(x2+y2)3/2/(xy-yx)式中：x=dx/dδ,y=dy/dδ,x=d2x/dδ2,y=d2y/dδ2若不满足此条件时：增大r0减小rr青岛科技大学专用作者：潘存云教授 作者：潘存云教授123456788’7’6’5’4’3’2’1’9’10’11’12’13’14’1514131211109ωωr04.平底尺寸l的确定lmaxa)作图法确定：l=2lmax+(5~7)mm青岛科技大学专用作者：潘存云教授 作者：潘存云教授δvCr0Oxyωds/dδlmax=[ds/dδ]maxP点为相对瞬心，有：b)计算法确定：BC=OP=v/ω=[ds/dt]/[dδ/dt]=[ds/dδ]l=2[ds/dδ]max+(5~7)mmv=OP·ωB0-ωs0sPBv青岛科技大学专用作者：潘存云教授 作者：潘存云教授对平底推杆凸轮机构，也有失真现象。Or0可通过增大r0解决此问题。r0青岛科技大学专用作者：潘存云教授 小结：在进行凸轮廓线设计之前，需要先确定r0,而在定r0时，应考虑结构条件（不能太小）、压力角、工作轮廓是否失真等因素。在条件允许时，应取较大的导轨长度L和较小的悬臂尺寸b。对滚子推杆，应恰当选取rr，对平底推杆，应确定合适的平底长度l。还要满足强度和工艺性要求。本章重点：①从动件运动规律：特性及作图法；②理论轮廓与实际轮廓的关系；③凸轮压力角α与基圆半径r0的关系；④掌握用图解法设计凸轮轮廓曲线的步骤与方法；⑤掌握解析法在凸轮轮廓设计中的应用。青岛科技大学专用作者：潘存云教授 疟疾 一、定义是感受疟邪引起的以寒战、壮热，头痛、汗出，休作有时为临床特证的一类疾病。 二、病名源流殷虚甲骨文中已有“疟”字。疟疾病名首见《内经》。《素问》有“疟论”与“刺疟”专篇。《金匮要略·疟病脉证并治》有“瘅疟、温疟、牝疟”以及“疟母”等不同类型的疟疾。《诸病源候论》之“间日疟候”与“劳疟候”等篇章中提出“间日疟”与“劳疟”名称。《三因极一病证方论·疟病不内外因证治》明确“疫疟”。《症因脉治·疟疾总论》进一步论述了“瘴疟”，并将间二日而发之疟称为“三日疟”。《疟疾论》将“三日疟”称为“三阴疟”，其特点是患病时间较长，但病情相对较轻，“无骤死之理”。 三、范围本病与西医疟疾等同。但西医学中回归热、黑热病、病毒性感染以及部分血液系统疾病等表现为寒热往来、似疟非疟者，也可参照治疗。 四、病因病机『病因』主要是感受“疟邪”。引起瘴疟者为瘴毒或瘴气，岭南（今广东）多见。『病机』发病：与卫气相集则引起发病，与卫气相离则病休（“入而与阴争则寒，出而与阳争则热”）。病位：疟邪内舍于营气，伏藏在半表半里（皮肤之内，肠胃之外）----邪在少阳----“疟不离少阳”。病性：“邪气盛则实”，此病为感“疟邪”所致，因此病理性质以邪实为主。但疟邪久留，疟疾发而不止，必伤气血，则属邪实正虚的虚实夹杂之证。病势：随经络而内搏五脏，横连募原 。 疟疾的分类：疟邪的盛虚更替，疟气的浅深，疟行之迟速，决定着与卫气相集的周期而病以时作的特点，此以发作周期而分型的疟以间日一作者最为多见；疟气深而行更迟者，则间二日而发，形成三日疟或称三阴疟。不同的体质，感受不同的疟邪，表现出阴阳偏盛、寒热多少的不同， 而有不同的分类： ①正疟：通常情况下形成的以寒热休作有时为特点者。②温疟：素体阳热偏盛，或感受暑热诱发，表现为热多寒少的疟疾。③寒疟：素体阳虚寒盛，或感受寒湿诱发，表现为寒多热少或但寒不热（牝疟）的疟疾。④瘴疟：感受山岚瘴毒所致，阴阳极度偏盛，心神蒙蔽，表现为寒热偏颇，神昏谵语者。热邪深重，内陷心肝者为热瘴，湿浊蒙蔽心神者为冷瘴。⑤劳疟：疟疾久发，气血耗伤，疟邪久羁，遇劳而发者。 五、诊查要点『诊断依据』1.发作时寒战、高热，出汗则热退，呈每日或隔日或三日发作1次的周期性发作，可伴有头痛身楚，恶心呕吐等症状。间歇期症状消失。2.夏秋季节发病，居住在流行地区或流行地区接触史。3.反复发作后可出现脾脏肿大。 证侯特证：寒战----寒冷期10分钟～1小时。高热----发热期4小时～8小时。休作有时----每日、隔日或三日定时而发。伴随症状：头痛、出汗（出汗期2小时～3小时），汗出则热退。夏秋季节多发。 『病证鉴别』1.疟疾与风温发热：风温发热多在冬春，邪在卫分，寒战发热而不具“往来”之特点；邪未伏藏，发病不呈休作有时的特点；“温邪上受，首先犯肺”，因此一般有咳嗽气急、胸痛等肺系症状。2.疟疾与淋证发热：淋证初起，湿热蕴蒸，邪正相搏，常有寒战发热，但病为邪壅膀胱，气化不利，有小便频、急、滴沥刺痛等表现。 3.寒疟、温疟与瘴疟：寒盛，寒重热轻，或但寒不热者为寒疟；热盛，热多寒少，或但热不寒者为温疟；热盛寒微或寒盛热微，神志昏迷者为瘴疟，或为热瘴，或为冷瘴。『相关检查』血涂片或骨髓片查获疟原虫为确诊依据。 六、辨证论治『辨证要点』分清正疟、温疟、寒疟、瘴疟、劳疟之不同。主要依据是病情轻重，寒热偏盛，正气的盛衰，病程的久暂。 『治疗原则』基本原则----祛邪截疟。正疟：和解表里温疟：清热保津寒疟：温阳达邪瘴疟：热瘴----清心开窍，冷瘴----化浊开窍劳疟：补益气血疟母：祛瘀化痰软坚『分证论治』 正疟症主症为疟疾典型发作：常先有呵欠乏力，继则寒战鼓颔，寒罢则内外皆热，头痛面赤，口渴引饮，继则遍身汗出，热退身凉，每日或间一二日发作一次，寒热休作有时。舌、脉：舌红，苔薄白或黄腻，脉弦。理疟邪伏于少阳，与营卫相搏，正邪交争。法祛邪截疟、和解表里。方柴胡截疟饮或七宝截疟饮药柴胡截疟饮（小柴胡+常山、槟榔、乌梅、桃仁）七宝截疟饮（常山、槟榔、草果、厚朴、青皮、陈皮、甘草） 温疟症主症：疟疾，发作时热多寒少。兼有表邪未解者：汗出不畅，头痛，骨节酸痛。热邪深重：口渴引饮，便秘尿赤。舌、脉：舌红苔黄，脉弦数。理阳热素盛，疟邪与营卫相搏，热炽于里。法清热解表、和解祛邪。方白虎加桂枝汤或白虎加人参汤加减药 寒疟症主症：疟疾，发作时热少寒多。寒湿内盛证：口不渴，胸闷脘痞，神疲体倦。舌、脉：舌苔白腻，脉弦。理素体阳虚，疟邪入侵，寒湿内盛。法和解表理、温阳达邪方柴胡桂枝干姜汤合截疟七宝饮加减药 瘴疟----热瘴症主症：热甚寒微，或壮热不寒，神昏谵语。瘴毒侵袭：头痛，肢体烦疼，胸闷呕吐。邪热内盛：面红目赤，烦渴饮冷，大便秘结，小便热赤。舌、脉：舌质红绛，苔黄腻或垢黑，脉洪数或弦数理瘴毒内盛，邪热内陷心包。法解毒除瘴、清热保津。方清瘴汤加减。药蒿芩清胆汤+常山、黄连、柴胡、知母，方中碧玉散换成益元散 瘴疟----冷瘴症主症：寒甚热微，或但寒不热，甚则嗜睡不语，神志昏蒙。湿浊证：如呕吐腹泻。舌、脉：舌苔厚而白腻，脉弦。理瘴毒内盛，湿浊蒙蔽心窍。法解毒除瘴、芳化湿浊方加味不换金正气散药不换金正气散（平胃散+半夏、藿香）+佩兰、草果、槟榔、石菖蒲、荷叶 劳疟症主症：疟疾迁延不愈，每遇劳累辄复发，发时寒热较轻。气血亏虚证：面色萎黄，倦怠乏力，短气懒言，纳少自汗。舌、脉：舌质淡，脉细弱。理疟邪久羁，气血耗伤。法益气养血、扶正祛邪方何人饮药何首乌、人参、当归、陈皮、生姜 恶性疟（脑型2%；肺型：急性肺水肿而呼衰；胃肠型；肾型；黄疸弛张型；厥冷型）。青蒿素对各种疟原虫的红内期无性体均有作用。对脑型疟与抗氯喹的恶性疟有良好疗效，原有片剂与水混悬液，目前使用浸膏片0.2(2#)、bid×4；青蒿素油注射液0.2(0.1/2ml/支)，im，按0h、6h、24h、48h四个时段共用4次。疟母：为久疟不愈，痰浊瘀血互结，左胁下形成之痞块（慢性疟疾肿大的脾脏，治疗后不缩小，遇暴力易破裂；急性期有轻中度肿大）。治宜软坚散结、祛瘀化痰。方用鳖甲煎丸。 其它疗法 转归预后 预防与调摄 结语'