最新Z变换(1)课件PPT.ppt 63页

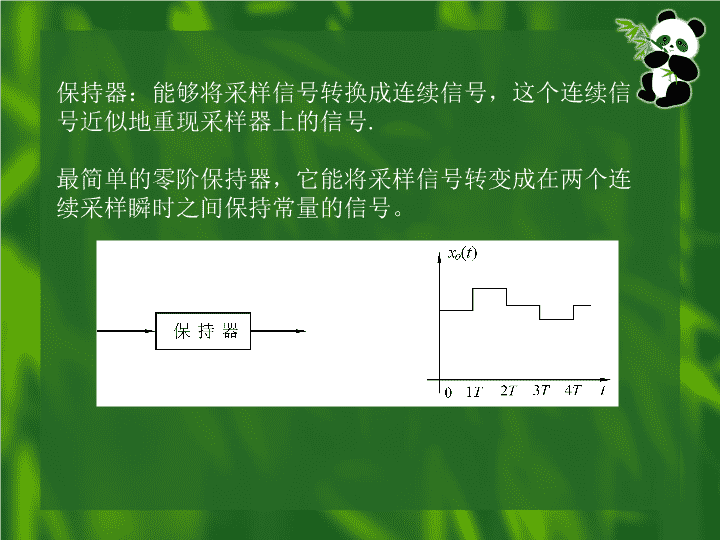
'Z变换(1) 10.1Z变换10.1.1采样器和保持器普通的采样器每间隔T秒钟开关闭合一次，使输入信号通过一次，即采样一次。采样器的功能是将连续信号转换成发生在采样瞬时刻0，T，2T，3T，…的一连串脉冲信号， 保持器：能够将采样信号转换成连续信号，这个连续信号近似地重现采样器上的信号.最简单的零阶保持器，它能将采样信号转变成在两个连续采样瞬时之间保持常量的信号。 因为在z变换中只考虑瞬时的信号，所以x(t)的z变换与x*(t)的z变换结果相同，即求Z变换的一般步骤为1)先求采样信号的Laplace变换，即2)将代入得Z[x(t)]。 例1.试求单位阶跃函数的z变换。解： 例2.求函数的z变换.解:查z变换表，的z变换为的z变换为 10.1.3留数定理求Z变换 10.1.4Z变换的性质1.线性定理设则 设函数x(t)的z变换为X(z)，并有极限存在则2.初值定理 3.终值定理 4.实数位移定理设x(t)的Z变换为X(z)，则滞后定理超前定理 5.复数位移定理设x(t)的Z变换为X(z)，则 10.2Z逆变换z逆变换记显然，z逆变换求出的是采样信号x*(t)，而不是连续信号x(t).确定离散控制系统时间响应要进行Z逆变换 10.2.1逆变换公式已知Z变换为X(z)，则可以证明在t=kT瞬时的采样函数值x(kT)，可以用下式来确定。等号右边的积分可按留数定理来确定，其中S表示包围全部极点的封闭曲线，即极点处的留数 X(z)一般可以表示为两个有理多项式之比对X(z)直接做长除法，用分母去除分子，并将商按z-1的幂次排列上式的z反变换为Cn(n=0，1，2…..）即为x(t)在采样时刻t=nT时的值x(nT).10.2.2幂级数法求Z逆变换 例10-18求的逆变换。解利用综合除法得 将z变换函数X(z)展开成部分分式之和，然后查z变换表，求相应的x*(t)。考虑到z变换表中，X(z)在其分子上普遍有因子z，所以应将X(z)/z展开成部分分式，然后将所得结果的每一项都乘以z，即得X(z)的部分分式。10.2.3部分分式展开法 例求的逆变换。解先将X(z)/z展开成部分分式所以 故查z变换表 10.3Z变换求差分方程对于一个控制系统的差分方程，首先利用Z变换，将差分方程变换为以z为自变量，X(z)为因变量的代数方程，解出X(z)后再进行Z逆变换，即可得到x(k)的值。 例10-22求下列差分方程的解式中解时代入方程得对差分方程进行Z变换，并考虑初始条件得 故又注意x(0)=0故 10.4脉冲传递函数1.脉冲传递函数的定义与求解离散控制系统的瞬态过程，其通用差分方程为两端取Z变换得故离散控制系统的传递函数为 称为脉冲传递函数。脉冲传递函数的求法如下1.求出系统的传递函数G(s);2.求出脉冲响应函数3.计算或求出系统传递函数G(s)后，将G(s)展开成部分分式之和，查Laplace变换与Z变换对应表，即可得到系统的脉冲传递函数。 例已知某系统的传递函数为求系统的脉冲传递函数。解：将G(s)展开成部分分式之和得查表得 2.串联开环系统的脉冲传递函数a.串联环节之间有理想开关 分别为线性环节的脉冲传递函数，和所以串联环节的脉冲传递函数为被理想开关隔断的两个串联环节的开环系统，其脉冲传递函数等于两个串联环节各自的脉冲传递函数的乘积。这个结论可以推广到有n个理想开关隔开的n个环节串联的开环系统，这时，整个系统的开环脉冲传递函数等于每个环节的脉冲传递函数的乘积，即 b.串联环节之间没有理想开关设则开环脉冲传递函数为表示先乘积后进行z变换。 两个线性环节相串联的开环系统，且环节之间无理想开关隔开时，开环系统的脉冲传递函数等于两个环节传递函数先乘积后再进行Z变换。显然，当有n个环节相串联，且环节之间无理想开关隔开时，此时系统开环脉冲传递函数等于n个环节传递函数先乘积后再进行Z变换，即通常即对于所有类似的系统，只要理想开关的位置不同，则它们的脉冲传递函数就不同。 10.5有零阶保持器的开环脉冲传递函数有零阶保持器传递函数为：Ga(s)为系统其它连续部分的传递函数 因为系统输出响应x0*(t)中包含两个分量：一个是输入采样信号xi*(t)经过G2(s)所产生的响应x01*(t)，它所对应的z变换另一个是输入采样信号xi*(t)经过e-TsG2(s)所产生的响应x02*(t)，由于e-Ts是延迟一个采样周期的延迟环节，因此x02*(t)比x01*(t)延迟一个采样周期， 根据z变换的实数位移定理，x02*(t)的z变换为所以有零阶保持器的脉冲传递函数为 例求图示的某离散控制系统的脉冲传递函数。解由图可得查表得 有零阶保持器的开环脉冲传递函数 10.6闭环系统的脉冲传递函数1)求图示的闭环系统的脉冲传递函数。 闭环脉冲传递函数 2)求图示的闭环系统的脉冲传递函数 解不出但可求出输出响应式。 例求如图所示的闭环系统的单位阶跃响应。解根据表10-2可得图示的闭环系统输出响应的z变换为又因 因此可得因为输入为单位阶跃响应 由此可得xo(k)与k的离散点 10.7脉冲系统的稳定性分析首先研究Z平面与s平面的映射关系根据Z变换的定义在s平面上 当，则对应在s左半平面，系统稳定映射到Z平面上对应在Z平面的单位圆内，脉冲系统稳定；当>，则对应在s右半平面，系统不稳定，映射到Z平面上对应在Z平面的单位圆外，脉冲系统不稳定；当＝，则对应在s平面的虚轴上，系统临界稳定，映射到Z平面上对应在Z平面的单位圆上，脉冲系统临界稳定。 稳定性分析首先假设系统的闭环脉冲传递函数为欲使系统稳定，则由特征方程的根来确定。如果系统稳定，则特征方程式的根全部落在单位圆内，即如果系统不稳定，则特征根至少有一个根落在单位圆外。如果系统临界稳定，则特征根至少有一个或多个根落在单位圆上，其余的根全部落在单位圆内 判别Z的多项式的根是否在单位圆内，用Routh稳定性判据方法确定。Routh判据应用在Z平面上借助于下列w变换，即将此变换代入特征方程，得到自变量w的特征多项式，再根据Routh判据规则，确定系统的稳定性。 例10-29确定如图10-14所示的系统的稳定性。解因为 特征方程为应用变换 根据Routh判据规则只要求即可满足稳定性条件所以 奇怪的大石头 李四光，中国地质事业的奠基者和领导人。他毕生从事地质科学的研究和教育事业，成就卓著，蜚声海内外，是我国冰川学研究的奠基人。他独创的地质力学理论，为我国的地质、石油勘探和建设事业做出了巨大贡献。( 陨石：大的流星在经过地球大气层时，没有完全烧毁坠落到地球上的含石质较多或全部为石质的陨星。地质学家：从事地球物质形成和地壳构造研究，以探讨地球的形成和发展的科学家。突兀：高耸。 第四纪：地质历史的最后一个纪。约从距今250万年前至今。此时高纬度地区广泛地发生了多次冰川作用。秦岭：横贯我国中部，东西走向的古老褶皱断层山脉。我国地理上的南北分解线。分布有冰川槽谷、角峰等。 冰川：在高山或两极地区，积雪由于自身的压力变成冰块（或积雪融化、下渗冻结成冰块），又因重力作用而沿着地面倾斜方面移动，这种移动的大冰块叫做冰川。在地质上的新生代第四纪，气候非常寒冷，世界上的许多地方被冰川覆盖，称第四纪冰川。 北极冰川 北极科学家拍摄到的海上冰川 第四纪冰川遗迹 唐古拉山冰川 奇怪著名悄悄躲闪兴趣历史平整旅行专门考察秦岭遗迹研究成果震惊卧室土坑推测世纪纪念地质学家严严实实捉迷藏转来转去 坑藏考秦域遗震著悄闪卧推旅纪究 思考：1、奇怪的大石头，“怪”在哪里？2、李四光是如何思考和解决自己的问题的？'