最新八上第三章《物态变化》PPT课件PPT课件.ppt 66页

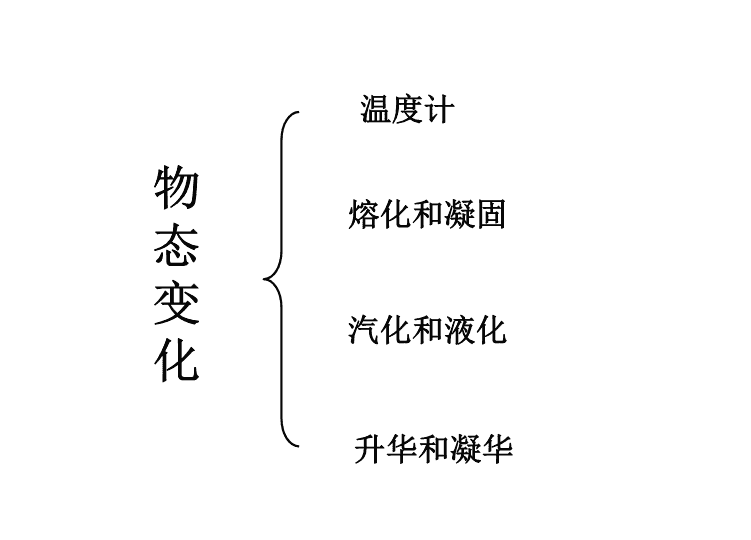
'八上第三章《物态变化》PPT课件 复习目标1、能够正确使用温度计2、知道物态变化的几种类型3、知道生活中物态变化的实例 物态变化温度计汽化和液化升华和凝华熔化和凝固 1、定义：吸、放热情况温度变化情况状态AB段BC段CD段特点：吸热上升固态吸热不变固液共存吸热上升液态温度达到熔点，继续吸热继续吸热，温度不变辨析：48℃的海波是什么状态？物质由固态变成液态的过程叫做熔化2、固体分为晶体和非晶体两类／3、晶体熔化条件：举例：海波、萘、冰、各种金属、水晶、食盐、萘、石英等熔化 1、定义：吸、放热情况温度变化情况状态EFFGGH特点：放热下降液态放热不变固液共存放热下降固态温度达到凝固点，继续放热继续放热，温度不变物质由液态变成固态的过程EFGH凝固点2、晶体凝固条件：凝固 例１、在图中的四个图象中，表示萘熔化的图象是（）例2、将冰、水组成的混合物放在0℃的房间内，经过足够长的时间，观察到的物态变化是（）A.水全部结成冰B.冰全部化为水C.水不结成冰，冰也不化为水D.以上三种情况都有可能典型例题考点：晶体和非晶体熔化、凝固的区别DC 例3、对海波粉加热时，它的温度随时间变化的图象如图所示，从图中可以看出：（1）海波粉的熔点是_________；（2）图中AB段表示海波处于____态；BC段表示海波处于______态。（3）海波熔化过程用了_______分钟。（4）实验采用的是加热。好处：。02814t/minABCD48℃t/℃48℃固固液共存6水浴使物质受热均匀 固态液态熔化（吸热）凝固（放热）汽化（吸热）液化（放热）升华（吸热）凝华（放热）气态知识回顾---物态变化 知识回顾-----汽化1、定义：温度下在液体的进行的比较的汽化现象。液体表面的气流速度物质由变成的过程。2、方式：和。3、蒸发液态气态蒸发沸腾定义：◆表面缓慢任何影响快慢的因素：◆液体的温度液体的表面积需要热量。吸收 温度下，在液体的同时进行的的汽化现象。4、沸腾知识回顾-----汽化定义：◆一定表面和内部剧烈◆实验---水沸腾实验器材：铁架台、酒精灯、石棉网、烧杯、温度计、秒表、纸盖 大量气泡不断、，到水面破裂开来，里面的散发到空气中。图象：现象：条件：特点：达到沸点不断吸热不断吸热温度不变知识回顾-----汽化ABC沸点t/minT/℃上升变大水蒸气缩短加热时间的方法：1、用较少的初温较高的水2、给烧杯加纸盖 5、蒸发和沸腾的比较异同点蒸发沸腾不同点发生部位温度条件剧烈程度影响因素供热快慢温度变化降温致冷吸收热量，温度不变相同点液体表面任何温度达到沸点缓慢液体表面和内部剧烈温度、表面积、气体流速都是汽化现象、都需要吸热知识回顾-----汽化 例1、下面能使蒸发变慢的措施是（   ）A.用瓶子装酒精时要加盖B.塑料袋包装蔬菜放入冰箱冷藏室内C.夏天,人们使用电风扇扇风D.把湿衣服展开晾在通风向阳处B例2、如图所示，将甲、乙两个试管装水后分别放入两个盛有水的容器内。乙试管所置的容器有密封的盖子。若对容器加热使容器内的水沸腾，下列说法中正确的是（）A.甲、乙两试管内的水都沸腾B.甲、乙两试管的水都不沸腾C.甲管内的水沸腾，乙管内的水不沸腾D.甲管内的水不沸腾，乙管内的水沸腾典型例题D 例3、在“观察水的沸腾”实验中(1)如图甲是某同学选用温度计测小烧杯中水的初温的操作图。A是操作过程，B是读数过程，C是读取的温度。①A图中操作的错误是：。②B图读数中的错误是：。③若操作正确无误，由C图可知此时烧杯中水实际温度是℃(2)图乙是该同学在做实验时，发现水从加热到沸腾所用时间过长，请你帮助他找出两种可能存在的原因。①；②。温度计的玻璃泡碰到了烧杯底读数时温度计的玻璃泡离开了被测液体30水太多水的初温较低甲乙甲乙 2、液化的两种方式:1、定义：降低温度压缩体积物质由变成的过程。气态液态知识回顾-----液化此过程需要热。放 3、生活中的一些液化现象雾露“白气”啤酒瓶“出汗”室外到室内，镜片“模糊”云 例1、下面现象中属于液化现象的是(   )   A.冬天人呼出的“白气”B.冬天湖面上结了冰C.春天冰雪消融D.夏天在室内洒水降温例2、烧水时从壶嘴里喷出“白气”，形成“白气”的物态变化过程是（）A．液化过程B．汽化过程C．先汽化后液化D．先液化后汽化AC典型例题 知识回顾-----升华1、定义：物质由直接变成的过程。固态气态该过程需要热。吸2、生活中的升华现象：樟脑丸变小冰冻的衣服直接变干灯丝用久变细碘颗粒变成碘蒸气用干冰冷藏物品、人工降雨、制造舞台烟雾 知识回顾-----凝华1、定义：物质由直接变成的过程。该过程需要热。气态固态放2、生活中的凝华现象：用久的灯泡变黑霜雪雾凇冰花（先升华后凝华） 例1、下面现象中属于升华现象的是(   )   A.冬天人呼出的“白气”B.初冬早晨草叶上的白霜C.冬天室外冰冻的衣服干了D.冬天室外的水结冰C典型例题例2、水的三态变化冰水水蒸气（）（）（）（）（）（）熔化凝固汽化液化升华凝华 1.（2016•连云港）下列与物态变化有关的现象说法正确的是（　　）A．霜的形成是一种升华现象B．晶体熔化时吸收热量，温度升高C．衣柜里的樟脑丸逐渐消失是汽化现象D．烧开水时冒出的“白气”是水蒸气液化形成的2.（2016•武汉）关于热现象，下列说法正确的是（　　）A．干冰给食品保鲜，利用了干冰熔化吸热B．把酒精擦在手背上，感到凉爽，是由于酒精汽化放热C．从冰箱取出冷冻的水放一会，表面会变湿，是由于水蒸气液化D．北方的冬天，在菜窖里放几桶水，利用了水凝华放热实战演练DB 3.（2016•广州）将杯中的液态氮（沸点为﹣196℃）倒入盛有奶浆的碗制作冰淇淋，观察到杯中液态氮沸腾，杯外壁出现白霜，则（　　）A．杯中液态氮放热B．杯中液态氮温度不断上升C．杯中液态氮不断吸热，温度保持﹣196℃D．白霜是空气中水蒸气液化形成的C4.（2016年长沙）下列自然现象属于吸热变化是（　）A、早春江面上皑皑冰雪的消融B、初夏江面上浩浩浓雾的形成C、深秋江边上晶莹冰凌的生成D、初冬江岸上美丽雾凇的出现A 6.（2015年彬州）右图是海波的熔化图像，下列信息正确的是（）A海波的沸点是48℃B.海波在BC段吸收了热量C.海波在CD段是气态D.6min时海波已全部熔化5.（2016年杭州）下列物态变化中，属于液化现象的是（）A．春天，冰封的湖面解冻B．夏天，打开冰棍纸看到“白气”C．深秋，屋顶的瓦上结了一层霜D．冬天，冰冻的衣服逐渐变干ＢB 7.（2015年重庆）如图是某种物质熔化时温度的变化规律（烧杯内物质在相同时间内吸收的热量相同）。（1）根据实验数据描出加热过程中杯内物质的温度随时间变化图象如图，该物质的熔点是_______。（2）第2min，该物质处于态（选填“固”、“液”、“固、液共存”）（3）第2min与第3min相比，哪一时刻杯内物体内能较大？_______，理由是。（4）已知0～1min与4～5min的时间相等，由图可知两段时间内温度升高不同，由此可以做出：“这种物质固态时的比热容小于液态时的比热容”的判断。请写出做出此判断的依据。0℃固液共存第3min第3min吸收的热量多因为当吸收热量相同时，相同质量的冰比水温度变化大。 8.（2014年岳阳）如图所示，下列说法中正确的是()Ａ．甲图可能是海波熔化图象B．乙图可能是松香凝固图象C．丙图可能是萘熔化图象D．丁图可能是石英凝固图象Ａ9.（2014年福州）将酒精从水与酒精的混合液中分离出来，可以采用的方法是利用它们的（）A.密度不同B.体积不同C.熔点不同D.沸点不同D 10.（2014年泰安）干冰可以用来人工降雨，飞机喷洒干冰进入云层会很快＿＿＿＿，并从周围＿＿＿大量的热，使空气温度急剧下降，高空中的水蒸气便＿＿＿成小冰粒逐渐变大而下降，遇到暖气流就＿＿为雨滴降落到地上。升华吸收凝华熔化11.（2014年孝感）把烧红的铁块放入水中，会听到吱吱的响声并看到有“白气”冒出，这现象属于（）A、液化B、汽化C、先熔化后汽化D、先汽化后液化D 12、生活中常见的物态变化现象1、冬天嘴呼出的“白气”的形成——2、雾的形成——3、露的形成——4、霜的形成——5、用久日光灯管变黑——6、冰镇啤酒瓶“冒汗”——7、用久的电灯的灯丝变细——8、天空中云的形成——9、舞台上干冰形成的白雾——10、冰棒冒“白气”——11、烧开水时，水面冒出的“白气”——12、冰棒纸上结的“霜”——液化液化液化凝华先升华后凝华液化升华液化和凝华先升华后液化液化先汽化后液化凝华 欢迎指导谢谢大家 学习要点理解回溯法的深度优先搜索策略。掌握用回溯法解题的算法框架（1）递归回溯（2）迭代回溯（3）子集树算法框架（4）排列树算法框架32 通过应用范例学习回溯法的设计策略。（1）装载问题；（2）批处理作业调度；（3）符号三角形问题（4）n后问题；（5）0-1背包问题；（6）最大团问题；（7）图的m着色问题（8）旅行售货员问题（9）圆排列问题（10）电路板排列问题（11）连续邮资问题33 有许多问题，当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。回溯法回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。34 问题的解空间问题的解向量：回溯法希望一个问题的解能够表示成一个n元式(x1,x2,…,xn)的形式。注意：同一个问题可以有多种表示，有些表示方法更简单，所需表示的状态空间更小（存储量少，搜索方法简单）。n=3时的0-1背包问题用完全二叉树表示的解空间,其解空间为{(0,0,0),(0,1,0),(0,0,1),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)}定义了问题的解空间后,还应将解空间很好地组织起来,使得能用回溯法方便地搜索整个解空间,通常将解空间组织成树或图的形式35 生成问题状态的基本方法扩展结点:一个正在产生儿子的结点称为扩展结点活结点:一个自身已生成但其儿子还没有全部生成的节点称做活结点死结点:一个所有儿子已经产生的结点称做死结点深度优先的问题状态生成法：如果对一个扩展结点R，一旦产生了它的一个儿子C，就把C当做新的扩展结点。在完成对子树C（以C为根的子树）的穷尽搜索之后，将R重新变成扩展结点，继续生成R的下一个儿子（如果存在）回溯法在搜索解空间树时,通常采用两种策略避免无效搜索:其一是用约束函数在扩展结点处剪去不满足约束的子树;其二是用限界函数剪去得不到最优解的子树.这两类函数统称为剪枝函数.36 回溯法的基本思想回溯法的解题步骤:(1)针对所给问题，定义问题的解空间；(2)确定易于搜索的解空间结构；(3)以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。37 递归回溯回溯法对解空间作深度优先搜索，因此，在一般情况下用递归方法实现回溯法。voidbacktrack(intt){if(t>n)output(x);elsefor(inti=f(n,t);i<=g(n,t);i++){x[t]=h(i);if(constraint(t)&&bound(t))backtrack(t+1);}}38 迭代回溯采用树的非递归深度优先遍历算法，可将回溯法表示为一个非递归迭代过程。voiditerativeBacktrack(){intt=1;while(t>0){if(f(n,t)<=g(n,t))for(inti=f(n,t);i<=g(n,t);i++){x[t]=h(i);if(constraint(t)&&bound(t)){if(solution(t))output(x);elset++;}}elset--;}}39 迭代回溯用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻，算法只保存从根结点到当前扩展结点的路径。如果解空间树中从根结点到叶结点的最长路径的长度为h(n)，则回溯法所需的计算空间通常为O(h(n))。而显式地存储整个解空间则需要O(2h(n))或O(h(n)!)内存空间。40 子集树与排列树遍历子集树需O(2n)计算时间遍历排列树需要O(n!)计算时间voidbacktrack(intt){if(t>n)output(x);elsefor(inti=0;i<=1;i++){x[t]=i;if(legal(t))backtrack(t+1);}}voidbacktrack(intt){if(t>n)output(x);elsefor(inti=t;i<=n;i++){swap(x[t],x[i]);if(legal(t))backtrack(t+1);swap(x[t],x[i]);}}41 装载问题有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且装载问题要求确定是否有一个合理的装载方案可将这n个集装箱装上这2艘轮船。如果有，找出一种装载方案。例如,当n=3,c1=c2=50,且w=[10,40,40]或者w=[20,40,40]42 装载问题容易证明，如果一个给定装载问题有解，则采用下面的策略可得到最优装载方案。(1)首先将第一艘轮船尽可能装满；(2)将剩余的集装箱装上第二艘轮船。将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近。由此可知，装载问题等价于以下特殊的0-1背包问题。用回溯法设计解装载问题的O(2n)计算时间算法。在某些情况下该算法优于动态规划算法。43 装载问题算法设计:解空间：子集树可行性约束函数(选择当前元素)：voidbacktrack(inti){//搜索第i层结点if(i>n){//到达叶结点if(cw>bestw)bestw=cw;return;}if(cw+w[i]<=c){//搜索左子树x[i]=1;cw+=w[i];backtrack(i+1);cw-=w[i];}backtrack(i+1);//x[i]=0;}44 装载问题改进算法:上界函数(不选择当前元素)：当前载重量cw+剩余集装箱的重量r当前最优载重量bestwvoidbacktrack(inti){//搜索第i层结点if(i>n){bestw=cw;return;}r-=w[i];if(cw+w[i]<=c){//搜索左子树x[i]=1;cw+=w[i];backtrack(i+1);cw-=w[i];}if(cw+r>bestw){//x[i]=0;搜索右子树backtrack(i+1);}r+=w[i];}45 装载问题构造最优解:通过在类Loading中增加两个私有数据成员x和bestx。x用于记录从根至当前节点的路径；bestx记录当前最优解。46 装载问题迭代回溯:数组x记录了解空间树中从根到当前扩展结点的路径,这些信息已包含了回溯法在回溯时所需的信息。因此利用数组x所含的信息，可讲上述回溯法表示成非递归的形式。由此可进一步省去0(n)递归栈空间。47 批处理作业调度给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理，然后由机器2处理。作业Ji需要机器j的处理时间为tji。对于一个确定的作业调度，设Fji是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。tji机器1机器2作业121作业231作业323这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。48 批处理作业调度解空间：排列树voidFlowshop::Backtrack(inti){if(i>n){for(intj=1;j<=n;j++)bestx[j]=x[j];bestf=f;}elsefor(intj=i;j<=n;j++){f1+=M[x[j]][1];f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];f+=f2[i];if(fn)sum++;elsefor(inti=1;i<=n;i++){x[t]=i;if(Place(t))Backtrack(t+1);}}51 0-1背包问题解空间：子集树可行性约束函数：上界函数：templateTypepKnap::Bound(inti){//计算上界Typewcleft=c-cw;//剩余容量Typepb=cp;//以物品单位重量价值递减序装入物品while(i<=n&&w[i]<=cleft){cleft-=w[i];b+=p[i];i++;}//装满背包if(i<=n)b+=p[i]/w[i]*cleft;returnb;}52 最大团问题给定无向图G=(V，E)。如果UV，且对任意u，vU有(u，v)E，则称U是G的完全子图。G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。U是G的最大团当且仅当U是G的最大独立集。1245312453如果UV且对任意u，vU有(u，v)E，则称U是G的空子图。G的空子图U是G的独立集当且仅当U不包含在G的更大的空子图中。G的最大独立集是G中所含顶点数最多的独立集。对于任一无向图G=(V，E)其补图G=(V1，E1)定义为：V1=V，且(u，v)E1当且仅当(u，v)E。53 最大团问题解空间：子集树可行性约束函数：顶点i到已选入的顶点集中每一个顶点都有边相连。上界函数：有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。voidClique::Backtrack(inti){//计算最大团if(i>n){//到达叶结点for(intj=1;j<=n;j++)bestx[j]=x[j];bestn=cn;return;}//检查顶点i与当前团的连接intOK=1;for(intj=1;jbestn){//进入右子树x[i]=0;Backtrack(i+1);}}复杂度分析最大团问题的回溯算法backtrack所需的计算时间显然为O(n2n)。1245354 图的m着色问题给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。55 解向量：(x1,x2,…,xn)表示顶点i所着颜色x[i]可行性约束函数：顶点i与已着色的相邻顶点颜色不重复。图的m着色问题voidColor::Backtrack(intt){if(t>n){sum++;for(inti=1;i<=n;i++)cout<voidTraveling::Backtrack(inti){if(i==n){if(a[x[n-1]][x[n]]!=NoEdge&&a[x[n]][1]!=NoEdge&&(cc+a[x[n-1]][x[n]]+a[x[n]][1]temp)temp=valuex;}returntemp;}voidCircle::Compute(void){//计算当前圆排列的长度floatlow=0,high=0;for(inti=1;i<=n;i++){if(x[i]-r[i]high)high=x[i]+r[i];}if(high-lown)Compute();elsefor(intj=t;j<=n;j++){Swap(r[t],r[j]);floatcenterx=Center(t);if(centerx+r[t]+r[1]