最新《信号与系统》第八章--考研及期末考试课件PPT.ppt 88页

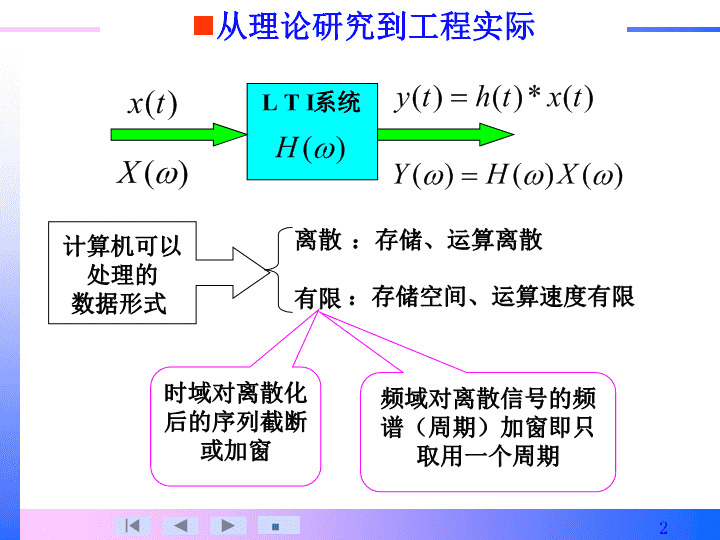
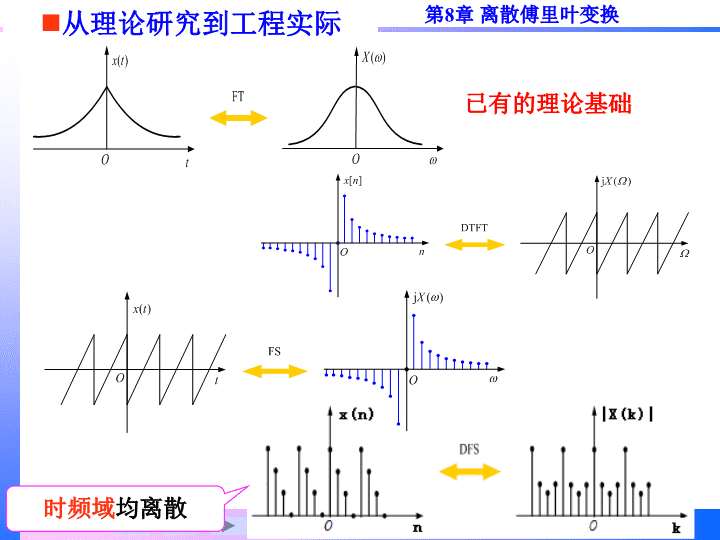
'《信号与系统》第八章--考研及期末考试 从理论研究到工程实际LTI系统计算机可以处理的数据形式离散有限：存储、运算离散：存储空间、运算速度有限时域对离散化后的序列截断或加窗频域对离散信号的频谱（周期）加窗即只取用一个周期 从理论研究到工程实际已有的理论基础时频域均离散 8.1.3DFT与DTFT和ZT变换的关系设x(n)是一个长度为N的有限长序列，则x(n)的离散时间傅里叶变换为将Ω离散化，在0~2π上从0开始等间隔地取N个点，即即可得到离散傅里叶变换DFT。对X(Ω)进行均匀采样，1.DTFT和DFT的关系X(k)是序列的傅立叶变换X(Ω)的在区间[0,2π]上的N点等间隔采样，采样间隔为：ΩN=2π/N。 为求DFT的反变换，将DFT两边乘以下面证明IDFT的唯一性并对k从0到N-1求和，得上式右边=Nx(n)n=0,1,…,N-1 2.DFT和Z变换的关系比较z变换与DFT变换，可见当设序列x(n)的长度为N，其z变换和DFT分别为：时，则有X(k)也是z变换在单位圆上的N点等间隔采样值，采样间隔为： 例求x(n)=R4(n)的DTFT及16点和32点的DFT。解根据DTFT的定义得其频谱为连续的，如图(b)所示 设变换区间N=16，则，n=0,1,…,15根据DFT的定义得 图6-1DFT与DTFT的关系图6-1(c)为16点DFT的频谱（实线），是离散的，实际上是对DTFT连续频谱离散化的结果，虚线是DTFT的频谱。图6-1(d)为32点DFT的频谱（其DFT变换省略）。 解：例 k＝1时，k≠1时，k＝7时，k≠7时， X(0)=X(2)=X(3)=X(4)=X(5)=X(6)=0当k=7时，当k=1时， 解： X(0)=X(2)=X(3)=X(4)=X(5)=X(6)=0当k=7时，DFT一般为复数当k=1时， 解：例 和分别为和的N点DFT.若和是两个有限长度序列，长度分别为和，则其线性组合的N点DFT为1.线性性质8.2离散傅里叶变换的性质 当k的取值不受限制时，X(k)以N为周期。2.DFT的隐含周期性 设x*(n)是x(n)的复共轭序列，长度为NX(k)=DFT[x(n)]则DFT[x*(n)]=X*(N-k),0≤k≤N-1且X(N)=X(0)3.复共轭序列的DFT证明：又由X(k)的隐含周期性有X(N)=X(0),它的末点就是它的起始点。用同样的方法可以证明DFT[x*(N-n)]=X*(k) 4.DFT的共轭对称性有限长共轭对称序列和共轭反对称序列有限长共轭对称序列：xep(n)=x*ep(N-n),0≤n≤N-1有限长共轭反对称序列：xop(n)=-x*op(N-n),0≤n≤N-1DFT的对称性是关于N/2点的对称性。注意：X(k)也是序列，对X(k)也成立。有限长共轭对称序列有限长共轭反对称序列 4.DFT的共轭对称性有限长共轭对称序列和共轭反对称序列有限长共轭对称序列：xep(n)=x*ep(N-n),0≤n≤N-1有限长共轭反对称序列：xop(n)=-x*op(N-n),0≤n≤N-1DFT的对称性是关于N/2点的对称性。注意：X(k)也是序列，对X(k)也成立。N/2左边N/2右边当N为偶数时，将上式中的n换成可得到 任何有限长序列x(n)都可以表示成其共轭对称分量和共轭反对称分量之和，即x(n)=xep(n)+xop(n),0≤n≤N-1将上式中的n换成N-n，并取复共轭，可得x*(N-n)=x*ep(N-n)+x*op(N-n)=xep(n)-xop(n)xep(n)=x*ep(N-n),0≤n≤N-1xop(n)=-x*op(N-n),0≤n≤N-1 1)如果x(n)=xep(n)+xop(n)，0≤n≤N-1其中4.DFT的共轭对称性 2)如果x(n)=xr(n)+jxi(n) 其中Xep(k)=DFT[xr(n)],是X(k)的共轭对称分量;Xop(k)=DFT[jxi(n)],是X(k)的共轭反对称分量。 用同样的方法可以证明具有共轭反对称性证明了Xep(k)=DFT[xr(n)]是X(k)的共轭对称分量。实际上 设x(n)是长度为N的实序列，且X(k)=DFT[x(n)]，对于纯实数序列，x(n)=xr(n)，X(k)只有共轭偶对称部分，即X(k)=Xep(k)，表明实数序列的DFT满足共轭对称性，故X(k)=X*(N-k)，0≤k≤N-1DFT[x(n)]=DFT[xr(n)]=X(k)=Xep(k)=X*ep(N-k)=X*(N-k)3)实信号DFT的共轭对称性 X(k)=X*(N-k)，0≤k≤N-1，利用这一特性，只要知道一半数目的X(k)，就可得到另一半的X(k)，这一特点在DFT运算中可以加以利用，以提高运算效率。4)DFT的共轭对称性的意义一次DFT变换两个实序列。将两个实序列，构成新序列x(n)如下：x(n)=x1(n)+jx2(n)对x(n)进行DFT，得到X(k)=DFT[x(n)]=Xep(k)+Xop(k)由Xep(k)=DFT[x1(n)]=1/2[X(k)+X*(N-k)]Xop(k)=DFT[jx2(n)]=1/2[X(k)-X*(N-k)]得X1(k)=DFT[x1(n)]=1/2[X(k)+X*(N-k)]X2(k)=DFT[x2(n)]=-j1/2[X(k)-X*(N-k)] 5．DFT的对偶性设长度为N的序列的DFT为，则 对应于DTFT的平移对应于DFT的移位m＝1m＝3m＝2圆周移位序列6.DFT的圆周（循环）移位性质 循环移位示意图右移出去的m个数据从左边补进来，数据不少，只是重新排队。 时域循环移位特性若时域序列的圆周位移的DFT为原来的DFT乘以一个因子则N为偶数时若则 频域循环移位特性若则在频域的频移l，则IDFT在时域x(n)乘以一个若则 若x(n)和h(n)均为N点有限长序列，且则N点的圆周卷积x(n)和h(n)都需是N点定义为圆周卷积两序列循环卷积的长度为N。7．DFT的时域离散圆周卷积定理 用DFT计算循环卷积则由时域循环卷积定理有Y(k)=DFT[y(n)]=X1(k)X2(k),0≤k≤N-1y(n)=IDFT[Y(k)]当L很大时,在频域计算提高了运算速度。 圆周卷积的计算特点圆卷积只在区间内进行，圆卷积结果也为N点有限长序列。x(m)是把x(n)变量代换后的N点序列，是把h(n)变量代换、圆反转、圆移位后，取其前N个点后的N点序列。对每一个n点圆移位，先计算对应各个m点的乘积，再对范围内的全部乘积求和。每一个n点圆周卷积的计算包括：变量代换、圆反转、圆移位、相乘、求和共5个步骤。以4点圆周卷积为例，全部过程可以用矩阵表示为： 时域圆周卷积定理圆周卷积5个步骤的图解举例：变量代换—圆反转—圆移位—相乘—求和例用图解法求有限长序列的4点圆卷积。解（1）变量代换x[n]、h[n]的变量置换为m，有（2）圆反转把h[m]圆反转为（3）圆移位—相乘—求和 时域圆周卷积定理解（3）圆移位—相乘—求和1234412342612相乘求和圆周卷积线性卷积 时域圆周卷积定理求和 圆周卷积5个步骤的图解举例：变量代换—圆反转—圆移位—相乘—求和例求有限长序列的4点圆卷积。解： 例用时域卷积定理求有限长序列的4点圆卷积。解 若则8．DFT的频域离散圆周卷积定理 实际问题多数是求解线性卷积，如信号x(n)通过系统h(n)，其输出就是线性卷积y(n)=x(n)*h(n)。而循环卷积比起线性卷积，在运算速度上有很大的优越性，它可以采用快速傅里叶变换（FFT）技术，若能利用循环卷积求线性卷积，会带来很大的方便。现在我们来讨论上述x(n)与h(n)的线性卷积，如果x(n)、h(n)为有限长序列，则在什么条件下能用循环卷积代替而不产生失真。8.3用DFT计算线性卷积 (1)有限长序列线性卷积与循环卷积的关系线性卷积：循环卷积为：8.3用DFT计算线性卷积 有限长序列x(n)为循环卷积为： 即 如果两个序列的长度分别为N和M，线性卷积后的长度为N+M-1，因此，如果循环卷积的长度L