最新应力状态与应变状态分析ppt课件PPT课件 44页

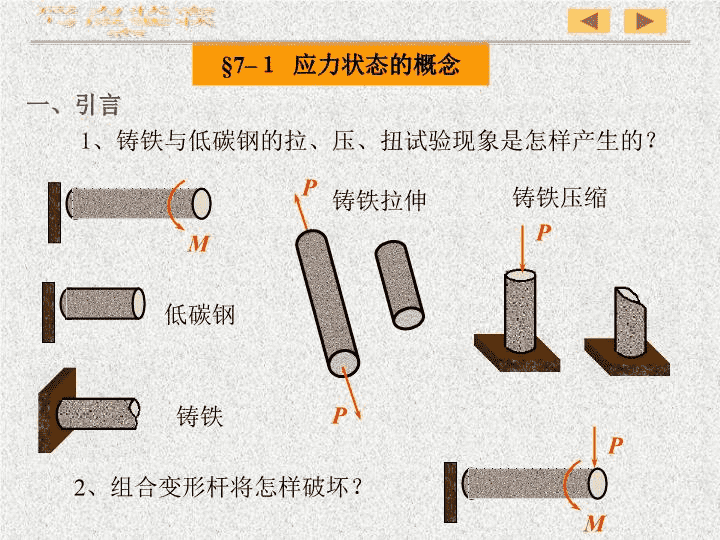
'应力状态与应变状态分析ppt课件 第七章应力状态与应变状态分析§7–1应力状态的概念§7–2平面应力状态分析——解析法§7–3平面应力状态分析——图解法§7–4梁的主应力及其主应力迹线§7–5三向应力状态研究——应力圆法§7–6复杂应力状态下的应力--应变关系——（广义虎克定律）§7–7复杂应力状态下的变形比能 §7–2平面应力状态分析——解析法应力状态与应变状态sxtxysyxyzxysxtxysyO 规定：截面外法线同向为正；ta绕研究对象顺时针转为正；a逆时针为正。图1设：斜截面面积为S，由分离体平衡得：一、任意斜截面上的应力应力状态与应变状态xysxtxysyOsytxysxsataaxyOtn图2 图1应力状态与应变状态xysxtxysyOsytxysxsataaxyOtn图2考虑剪应力互等和三角变换，得：同理： 二、极值应力´´应力状态与应变状态xysxtxysyO xysxtxysyO在剪应力相对的项限内，且偏向于x及y大的一侧。应力状态与应变状态222xyyxminmaxtsstt+-±=îí좢）（ 例2分析受扭构件的破坏规律。解：确定危险点并画其原始单元体求极值应力应力状态与应变状态txyCtyxMCxyOtxytyx 破坏分析应力状态与应变状态低碳钢铸铁 §7–3平面应力状态分析——图解法对上述方程消去参数（2），得：一、应力圆（StressCircle）应力状态与应变状态xysxtxysyOsytxysxsataaxyOtn此方程曲线为圆—应力圆（或莫尔圆，由德国工程师：OttoMohr引入） 建立应力坐标系，如下图所示，（注意选好比例尺）二、应力圆的画法在坐标系内画出点A(x，xy)和B(y，yx)AB与sa轴的交点C便是圆心。以C为圆心，以AC为半径画圆——应力圆；应力状态与应变状态sxtxysyxyOnsataaOsataCA(sx,txy)B(sy,tyx)x2anD(sa,ta) 应力状态与应变状态sxtxysyxyOnsataaOsataCA(sx,txy)B(sy,tyx)x2anD(sa,ta)三、单元体与应力圆的对应关系面上的应力(，)应力圆上一点(，)面的法线应力圆的半径两面夹角两半径夹角2；且转向一致。 四、在应力圆上标出极值应力应力状态与应变状态OCsataA(sx,txy)B(sy,tyx)x2a12a0s1s2s3 s3例3求图示单元体的主应力及主平面的位置。(单位：MPa)AB12解：主应力坐标系如图AB的垂直平分线与sa轴的交点C便是圆心，以C为圆心，以AC为半径画圆——应力圆0应力状态与应变状态s1s2BAC2s0sata(MPa)(MPa)O20MPa在坐标系内画出点 s3应力状态与应变状态s1s2BAC2s0sata(MPa)(MPa)O20MPa主应力及主平面如图102AB 解法2—解析法：分析——建立坐标系如图60°应力状态与应变状态xyO §7–4梁的主应力及其主应力迹线应力状态与应变状态12345P1P2q如图，已知梁发生剪切弯曲（横力弯曲），其上M、Q>0，试确定截面上各点主应力大小及主平面位置。单元体： 应力状态与应变状态21s1s3s33s1s34s1s1s35a0–45°a0stA1A2D2D1COsA2D2D1CA1Ot2a0stD2D1CD1O2a0=–90°sD2A1Ot2a0CD1A2stA2D2D1CA1O 拉力压力主应力迹线（StressTrajectories)：主应力方向线的包络线——曲线上每一点的切线都指示着该点的拉主应力方位（或压主应力方位）。实线表示拉主应力迹线；虚线表示压主应力迹线。应力状态与应变状态1313 qxy主应力迹线的画法：11截面22截面33截面44截面ii截面nn截面bacd13应力状态与应变状态31 §7–5三向应力状态研究——应力圆法应力状态与应变状态s2s1xyzs31、空间应力状态 2、三向应力分析弹性理论证明，图a单元体内任意一点任意截面上的应力都对应着图b的应力圆上或阴影区内的一点。图a图b整个单元体内的最大剪应力为：tmax应力状态与应变状态s2s1xyzs3 例4求图示单元体的主应力和最大剪应力。（MPa）解：由单元体图知：yz面为主面建立应力坐标系如图，画应力圆和点1′,得:应力状态与应变状态5040xyz3010(MPa)sa（MPa）taABCABs1s2s3tmax §7–6复杂应力状态下的应力--应变关系——（广义虎克定律）一、单拉下的应力--应变关系二、纯剪的应力--应变关系应力状态与应变状态xyzsxxyzxy 三、复杂状态下的应力---应变关系依叠加原理,得:应力状态与应变状态xyzszsytxysx 主应力---主应变关系四、平面状态下的应力---应变关系:方向一致应力状态与应变状态s1s3s2 主应力与主应变方向一致?应力状态与应变状态 五、体积应变与应力分量间的关系体积应变：体积应变与应力分量间的关系:应力状态与应变状态s1s3s2a1a2a3 例5已知一受力构件自由表面上某一点处的两个面内主应变分别为：1=24010-6，2=–16010-6，弹性模量E=210GPa，泊松比为=0.3，试求该点处的主应力及另一主应变。所以，该点处的平面应力状态应力状态与应变状态 me3342.-=应力状态与应变状态 例6图a所示为承受内压的薄壁容器。为测量容器所承受的内压力值，在容器表面用电阻应变片测得环向应变t=350×l06，若已知容器平均直径D=500mm，壁厚=10mm，容器材料的E=210GPa，=0.25，试求:1.导出容器横截面和纵截面上的正应力表达式；2.计算容器所受的内压力。应力状态与应变状态pppxs1smlpODxABy图a 1、轴向应力:(longitudinalstress)解：容器的环向和纵向应力表达式用横截面将容器截开，受力如图b所示,根据平衡方程应力状态与应变状态psmsmxD图b 用纵截面将容器截开，受力如图c所示2、环向应力：(hoopstress)3、求内压（以应力应变关系求之）应力状态与应变状态tm外表面ypststDqdqz图cO §7－7复杂应力状态下的变形比能231图a图c3-m1-m2-m应力状态与应变状态m图bmm 称为形状改变比能或歪形能。应力状态与应变状态图c3-m1-m2-m 例7用能量法证明三个弹性常数间的关系。纯剪单元体的比能为：纯剪单元体比能的主应力表示为：应力状态与应变状态txyA13 本章结束 结束语谢谢大家聆听！！！44'